Esempio

Ad ogni dito della mano destra ne corrisponde uno della mano sinistra e viceversa.
posso considerare che la mia mano sinistra sia l’insieme delle sue cinque dita, e la mano destra l’insieme di altre cinque dita.
Domanda: come posso fare per stabilire se questi due insiemi (le mani) contengono lo stesso numero di elementi (dita)? Posso contarli:
Oppure posso mettere in correlazione ciascun dito della mano sinistra con il rispettivo dito della mano destra:
In quest’ultimo caso ho messo in atto il concetto di "corrispondenza biunivoca": ad ogni elemento (dito) del primo insieme (mano sinistra) corrisponde uno ed un solo elemento (dito) del secondo insieme (mano destra), e viceversa. Avendo unito le dita delle due mani come si vede nella foto, posso affermare senza ombra di dubbio che la "potenza", o "cardinalità", o più semplicemente il numero di elementi contenuto da ciascuno dei due insiemi, è lo stesso. Non occorre contarli, non occorre affatto sapere quanti sono; la domanda era: hanno i due insiemi lo stesso numero di elementi? La risposta è senz’altro: Sì.
Esempio: regioni e capoluogo
Ad ogni regione corrisponde il suo capoluogo ed a ogni capoluogo corrisponde la sua regione.

Esempio: fette di torta e piattini
Ad ogni fetta di torta corrisponde il suo piattino e ad ogni piattino corrisponde la sua fetta di torta.



Se Marco mangia una fetta di torta non abbiamo più una corrispondenza biunivoca!
Esempio: asole e bottoni
Ad esempio, in una camicia, l’insieme delle asole e l’insieme dei bottoni sono in corrispondenza biunivoca:
ad ogni asola corrisponde uno e un sol bottone e viceversa ad ogni bottone corrisponde una e una sola asola.

Esempio: capitali e nazioni
Tra l'insieme delle capitali e l'insieme delle nazioni: una nazione ha una sola capitale,e una capitale è capitale di una sola nazione.

Esempio:i numeri naturali e i quadrati dei numeri naturali
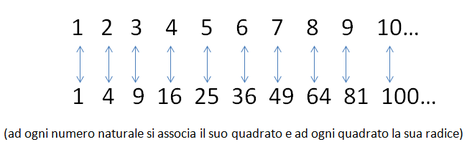
Pensando ai quadrati perfetti, si potrebbe pensare che sono infiniti, ma sicuramente meno dei naturali dal momento che mancano il 2, il 3, il 5 … In realtà sono ugualmente infiniti perché è possibile stabilire una corrispondenza biunivoca tra l’insieme dei naturali e l’insieme dei quadrati perfetti, cioè una corrispondenza nella quale ad ogni numero naturale corrisponda uno ed un solo quadrato.
Esempio: I numeri naturali e i numeri pari

Nel rispondere alle domande che chiedevano quanti sono i numeri pari e quelli dispari, avevamo ipotizzato che sono entrambi infiniti.
Anche per rappresentare questi abbiamo usato delle formule, in cui i numeri pari corrispondono a
2x
dal momento che ogni numero, moltiplicato per due, dà sempre come risultato un numero pari, e i numeri dispari corrispondono a
2x+1
quindi aggiungendo ad un numero pari una unità e facendo risultare un numero dispari.
Anche nel caso dei numeri pari si puo realizzare una corrispondenza biunivoca con i numeri naturali:
- ad ogni numero naturale possiamo associare il suo doppio (quindi un numero pari) che evidentemente è unico
- e viceversa ogni pari è l’immagine di un unico naturale.
 VIAGGIO
A MATHLAND
VIAGGIO
A MATHLAND
